




Next: 9 Health & Stability
Up: Part III: DEIMOS Calibration:
Previous: 7 Imaging - Procedures
Spectroscopic calibrations are complex, with added complexity from the
multislit nature of DEIMOS. We assume multislit throughout; longslit is
a special case of multislit.
This chapter deals with these elements:
- X-rectification:
- This operation removes x-distortion
-- distortion in the x-direction --
and is commonly referred to as ``straightening the spectra.''
(Note that this only applies to the spectrum of a slitlet; tilts in object
spectra due to atmospheric dispersion are not removed by this process.)
For simplicity, the operation is applied to all spectral data
before any other spectral calibration. We adopt a form:
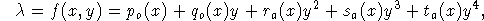
to describe the x-distortion pattern.
- Wavelength calibration:
- Assigning accurate wavelengths to each pixel
in a spectrum. Accuracy of assignment is TBD, but is expected to be
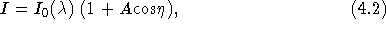 0.25
pixel or better. We assume the form:
0.25
pixel or better. We assume the form:

where the subscripts o and a denote derivation from the individual
observation or from the database archive, respectively.
We assume the spectra have already been x-rectified or straightened.
This functional form
describes the wavelength dependence for across an image; note that between
slitlets there will be a discontinuity in
the coefficient functions p(x), q(x), r(x), s(x), t(x),.
The general form requires knowledge of p, q, r, s, t as functions of
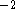 as well.
as well.
- Relative flux calibration:
- Adjusting counts along a spectrum and
between slits so that the same count-vs-flux ratio applies at a particular
wavelength.
- Absolute flux calibration:
- Conversion of count rates into physical
flux units. This consists of a ``sensitivity curve'' (spectrum) that converts
a count-rate at a given wavelength into units of
erg s
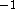 cm
cm  Å
Å 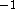 .
.
- Flat field:
- [To be written.]
Wavelength Calibration:
Internal arcs lamps cannot be used to precisely wavelength calibrate spectra
on the sky for these reasons:
- -
- Arc lamps don't illuminate optics the same as celestial objects;
- -
- Temporal instabilies change lambda scale;
- -
- Flexure effects;
- -
- Scale change with T; and
- -
- Scale change with focus
In addition, we don't want to take internal arc spectra during the night,
both because of loss of observing time and because the hatch must be closed,
which interrupts guiding.
However, spectra on the sky (particularly in the blue) will not always
include enough night sky lines of sufficient S/N to provide
a satisfactory wavelength solution. A hybrid calibration
-- using internal lamps for higher order terms and night sky lines for
lower-order terms --
is probably the most practical method to overcome these difficulties.
In practice, we propose that the coefficients r, s, t can be obtained
from internal arc spectra (and maintained in the database for pipeline
mode), and only the zeropoint and scale (p, q) come directly from the
science images using night sky lines. Our goal by this method is
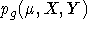 px.
px.
The coefficients are measured for each grating using a set of
``line-of-slitlets''
(LOS) masks to provide a grid of positions in the MF/SMCS. Spectra are
obtained and measured for each slit through a sequence of grating tilts.
For each grating, this gives a set of coefficients on a representative
grid in grating tilt ( 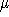 ) and slitmask coordinates (X,Y), that is,
) and slitmask coordinates (X,Y), that is,
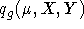
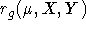
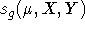

Note that, once x-rectified, there is a one-to-one correspondence between
X and x .
.
There are two options for database storage. First, the actual 3-D data cubes
(one per grating) can be stored. For reasonable values of gratings (5),
LOS masks (8), slits per mask (100) and grating tilts (12), this means
storing five data cubes of 9600 numbers each, or 48000 numbers total.
To retrieve coeeficients would involve interpolating in the appropriate
data cube.
The second method is to fit each data cube with an interpolating function
of the form:

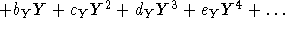
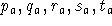
For five interpolating functions with 13 coefficients each, we need
to store only 65 numbers per grating, or 325 numbers total for five gratings.
The actual number of coefficients needed is TBD.
Flux Calibration: The grating introduces an additional degree of
complexity, partially by introducing an occasional vignetting that depends on
grating tilt, but most importantly because the camera will now vignette
some of the incoming beams. The vignetting at the grating itself,
however, will affect absolute but not relative flux calibration,
as the light is not yet dispersed. Furthermore, the camera vignetting is
a function of the grating reflection angle only, and it does not matter
if that angle is a result of dispersion, slitlet location, or both.
For this reason, we can use continuous spectra of a line-of-holes (LOH)
mask to map out the camera vignetting sufficient for relative flux calibration.
Here is a summary of the various components to spectral flux calibration:
- collimator/tent vignetting: this affects the overall flux
level, independent of wavelength, as a function of slitmask X,Y.
Use a direct flat to determine its effect, and apply to the entire spectrum.
- grating vignetting: only a problem for the large (
 )
grating at large tilts. Measurement TBD.
)
grating at large tilts. Measurement TBD.
- grating efficiency: can be measured through a series of
observations over various tilts for each grating. TBD: standard light source
appropriate for these measurements.
- camera vignetting: can be measured via LOH spectra.
- x-rectification: The user may use either a LOH mask or
even spaces between slits on a science slitmask, illuminated by internal lamp,
dome lamp or (preferably) the twilight sky to trace out slitlet edges and
solve for the x-distortion in (x,y).
- Wavelength Calibration:
In baseline mode, the user employs either internal arc spectra or
night sky lines to solve for the values of the coefficient functions
p(x), q(x), r(x), s(x), t(x). In practice, this will probably involve
internal arcs for r, s, t and night sky lines for the zeropoint and scale
p, q. Again, note that these coefficients will be
discontinuous in x between slitlets. A specific ``recipe'' follows:
- Obtain internal arc spectra through each mask with same grating,
tilt and order-separating filter as used for science exposures;
- X-rectify in same manner as science image;
- Y-rectify in same manner as science image, to straighten
emission lines; [Not described yet]
- Extract calibration spectra in same manner as object spectra;
- Measure line peaks to obtain y position for each arc line;
- Identify line wavelengths (arc and nightsky spectra and wavelengths
will be kept in the database);
- Solve for coefficients
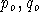 (here, ``a'' refers
to ``arc spectrum'');
(here, ``a'' refers
to ``arc spectrum''); - Extract night sky spectrum (or local arc) taken at same
position/time as science image (the S/N in the lines can be relatively low);
- Measure and identify emission lines;
- Solve for unknown coefficients
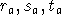 for each object spectrum,
assuming
for each object spectrum,
assuming 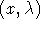 from previous fits.
from previous fits. - Extracted object spectrum is remapped onto a specified
 grid.
grid.
- Flux Calibration:
- x-rectification: The x-distortion map is retreived from the
database; image is remapped. [What about scale changes?].
- Wavelength Calibration:
Coefficients p, q, r, s, t are interpolated for
each x and
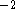 from information in the database .
Night sky lines (or internal arc at same position/time) are used to solve
for specific
from information in the database .
Night sky lines (or internal arc at same position/time) are used to solve
for specific 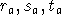 , assuming r, s, t from above.
Image is remapped onto a specified
, assuming r, s, t from above.
Image is remapped onto a specified  grid.
grid.
- Flux Calibration:
The database will contain a current x-distortion map;
for each grating, a 3-D table of coefficients 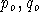 that can
be interpolated to specific values at a given (x,y) and
that can
be interpolated to specific values at a given (x,y) and 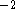 or interpolating functions for each grating to provide the same values;
[flux cal info, TDB].
or interpolating functions for each grating to provide the same values;
[flux cal info, TDB].
The database will also contain certain supplemental information:
- wavelength- and flux-calibrated spectra of each arc lamp
and the night sky, obtained with each grating;
- list of wavelengths for each arc lamp and the night sky;
- grating and order-separating filter information.
Required Hardware:
- -
- Line-of-slitlets (LOS) mask
- -
- Line-of-holes (LOH) mask
- 1.
- Obtain spectral images through LOS masks illuminated with an
appropriate arc source (appropriate means sufficient density of identified
spectral lines throughout the spectral region of interest). This requires,
for each grating, exposing through a set of LOS masks and a sequence of grating
tilts.
(Assuming 5 gratings, 8 LOS masks, 12 grating tilts, and 1 minute per
exposure, this means 480 exposures for a total time of 8 hr.)
- 2.
- X-rectify each image.
- 3.
- Extract the spectrum for each aperture in the LOS mask
(48000 spectra total).
- 4.
- Measure and identify lines in each spectrum and solve for the
coefficients p, q, r, s, t as functions of
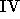 . Place in a 3-D table
for each grating and tilt (240000 coefficients total).
. Place in a 3-D table
for each grating and tilt (240000 coefficients total).
- [5.]
- Fit interpolating functions to the values of p, q, r, s, t as
functions of
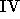 for each grating.
for each grating.
Instrument-control scripts and instructions to create the database products
listed above will be required.
As stated earlier, for flux calibration there is a need for a continuum light
source of constant spectral shape.
We need to discuss the effect of spatial distortion (different scales
throughout the image) on flux calibration. If the distortion is
mapable, there is no problem correcting the data for this.
We have not described slit functions (variations in throughput due to
irregularities in the slit shape). These must be mapped by the user for each
mask, and will be sensitive to plate scale changes, but their measurement
and removal is not expected to be a problem. Current milling practices
appear to reduce variations along the slit to less than about 1%.





Next: 9 Health & Stability
Up: Part III: DEIMOS Calibration:
Previous: 7 Imaging - Procedures
DEIMOS Software Team <deimos@ucolick.org>
1997-06-13T00:18:19
![]()
![]()
![]() as well.
as well.