The ultimate limit on positional accuracy is the photon noise
per FC spot. We assume that there is only one spot
visible in each FC CCD. The expected FWHM of a spot image
is about 0.5 (4.2 px), set by optical aberrations at the
FC CCDs near the edge of the camera FOV. For a Gaussian
PSF, the effective 1-d 
is 1.79 px.
For a rough calculation
of the expected S/N in a spot, we assume that the spot area is
4.2 
= 18 px , that
the readout noise of the FC CCDs is 5 e 
px 
(no binning),
and that the total number of detected photons N = 1000.
The effective photon noise under the image
in 18 px due to readout noise is 450 e .
If the readout noise is ignored, the 1-d rms positional error, 
,
is 1.79 px 
= 0.06 px. Subtracting the background
from each pixel increases the (photon noise) by 450/1000 = 45%,
which increases the positional error by 22% to 0.07 px. Both
of these errors are small compared to the final error budget of 0.25 rms
in each coordinate.
We conclude that a detected photon flux of 1000 counts and a CCD
RO noise of 5 e px are reasonable targets.
In spectroscopy mode, any translation of the image is accompanied by small optical distortions due to the reflection of the beam off a grating rather than a mirror. Each displacement of an optical element (e.g., the collimator mirror, tent mirror, grating, camera, or detector) has its own distortion pattern and magnitude. Residual errors in image position are introduced by the fact that distortions of the compensating elements (the tent mirror and detector) do not perfectly match the distortions of the other elements being corrected.
A rough rule of thumb is that an image motion of a given size is accompanied by an uncorrectable distortion that is 0.08 times as large. These residuals limit the largest bulk image correction that can be achieved by the FC system. For example, passive motions due to flexure may amount to as much as 2.5 px rms (see Section 1.1), inducing distortion errors that are 8% as large, or 0.20 px. This would take up essentially the whole error budget. We are striving to keep passive flexure a factor of two below this level, to leave room for other terms.
Note: This section is incomplete. It will be expanded in future to describe in detail the various kinds of optical distortions and compare them quantitatively with the expected motions of optical components.
Displacements of individual lens elements within the camera also cause position distortions. Flexure analysis of the camera indicates that these motions should be 10 times smaller than the effects noted above and can be ignored.
Because the corrections are computed only every 15 s, the correction will not be perfect even if the centroids are perfectly known. The maximum error occurs when the PA is changing rapidly, which occurs near zenith. Here the spectrograph rotates 180in approximately 5 minutes, the width of the alt-az dead zone. If we assume that the maximum peak-to-valley flexure of 5 px takes place in 5 minutes, a time lag of 15 s corresponds to an error of 0.25 px. This is large compared to the goal but exists over a short time only and could probably be reduced with a predictor-corrector scheme. We allot 0.05 px to this term.
Other correction errors should be small, as the system operates at low bandwidth compared to the bandwidth of the expected errors, and the gains of the active components should be highly stable over time after initial calibration.
The FC system is capable of steering the beam only - rotations and scale changes of the image are not corrected. We estimate here the errors introduced by these uncorrected terms.
A major lien against image stability is changes in the focal
length of the camera due to temperature changes. This is discussed
in the memo ``Change in DEIMOS
Plate Scale due to Thermal Effects," by S. M Faber (copies available).
The camera scale is exceedingly sensitive to temperature owing
to the use of positive-power thermally-sensitive CaF 
elements in conjunction
with negative-power glass elements that are much less sensitive
to temperature.
The fractional sensitivity of image scale to temperature
is -141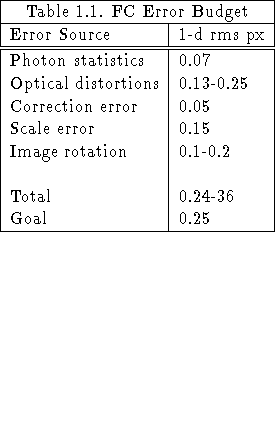 
per . If scale changes contribute no more than
0.1 px rms to the
image motion budget, the camera
temperature must be kept constant to 0.14
rms. The design operating temperature range is 
5 , so
this temperature constancy represents only 3% of the
expected temperature range.
The optical design is non-telecentric, so that slight changes of focus alter the scale. If advantage is taken of this effect, the requirement on temperature constancy might be relaxed somewhat, to 0.6 rms, though pushing this approach is not attractive owing to probable degradation of image quality. This relaxed tolerance represents 12% of the range.
We are attempting to compensate for the thermal scale change by altering the separation of two multiplets in the camera as a function of temperature. This separation would be controlled by a passive spacer whose length varies with temperature in the desired way. The allowed error of the correction is the same as the above percentage fraction of the temperature range. The main source of error in the passive approach is ignorance of the true physical constants of materials - the indices of refraction and coefficients of thermal expansion. A plausible error due to this ignorance is 10%. This is in between the most stringent specification of 3% but less than the maximally relaxed tolerance of 12%.
We adopt a final error of 10% for the passive correction and assume that we will use some degree of focus correction as an additional aid. Together they imply a final error of about 0.15 px rms from this term. If this scheme proves inadequate, we still have the option of adding some form of active thermal control to the camera optics.
The image may rotate on the detector owing to rotations of the detector itself, rotations of the camera holding the detector, and rotations of the grating. We allot 0.1-0.2 px to these terms, as suggested by results achieved from finite element analyses and prototypes of mounts that have been built.
The final error budget is given below:
These results suggest that, with care, the desired
stability goal of 0.25 px rms may be met but that attention to
every detail will be required. We note that the original goal
was developed with the most demanding
optical requirement in mind. Most optical images would be well preserved
if the goal were relaxed by a factor of two. Fringing also
degrades gracefully over this range. For a typical 600-line mm
grating yielding 0.66 Å/ mm , the
peak fringe flat-fielding error caused by an rms px shift of 0.5 px is
still less than 1% (SEE Part I, Section 4.3).
We conclude that meeting the image stability goal of 0.25 px rms will be difficult but that the help offered by the FC system is essential to approaching this goal.
The following sections are still in preparation: