




Next: 8 Spectroscopy - Procedures
Up: Part III: DEIMOS Calibration:
Previous: 6 CCDs - Procedures
This chapter deals with these elements:
- Flat field:
- An image of a uniformly illuminated (``flat'') field.
(In this section, ``flat field'' refers specifically to imaging mode.)
Flat field images will be assumed to be normalized to unity at a specified
``normalization point'' (which in practice will be a cosmetically-clean
region on the fiducial CCD). Flat fields are used to remove the signature
of the CCDs (``pixel-to-pixel variations'') and the system throughput
variations (``vignetting''; others?) across the field of view.
Flat fields are identified by their source of illumination --
twilight flats of the twilight sky,
dome flats of the dome illuminated by special lamps, and
internal flats of the hatch illuminated by lamps within DEIMOS.
In imaging mode, a flat field is alwyas associated with a particular filter
and is useful only with that filter.
- Fringe frame:
- A flat-fielded, normalized image of the dark sky (with
the continuum component subtracted),
showing a summation of interference fringes caused by strong night-sky emission
lines. The stability and/or utility of fringe frames is yet to be established.
- Relative flux calibration:
- Adjusting counts across an image to
the same count-vs-flux ratio. This is traditionally performed by division
by a flat field image, which has been normalized to unity at a specified
``normalization point.''
- Absolute flux calibration:
- Conversion of count rates into physical
flux units. This consists of two constants for each filter, a
zeropoint (
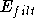 ) and an extinction coefficient (
) and an extinction coefficient ( 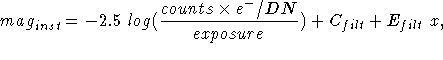 ).
The defining relation is:
).
The defining relation is:
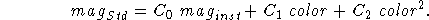
where x is the airmass at the time of observation.
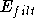 , sometimes refered to as total throughput
, sometimes refered to as total throughput ,
contains all the information about system efficiency or
throughput for the normalization point of the flat-field image.
,
contains all the information about system efficiency or
throughput for the normalization point of the flat-field image.
- Standard magnitudes:
- Magnitudes on a widely accepted system such
as Johnson UBV or the SDSS sytem. Conversion from instrumental to
standard magnitudes traditionally takes the form

The coefficients  ,
, 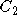 and
and 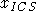 can be deduced from observations of
standard stars, or ``synthesized'' using measured transmission curves
and published spectral energy distributions for a wide range of spectral
types.
can be deduced from observations of
standard stars, or ``synthesized'' using measured transmission curves
and published spectral energy distributions for a wide range of spectral
types.
- Relative Astrometry:
- Determination of the relative positions,
in arcseconds on the sky, of positions in an image. This can be
expressed as a distortion mapping between the detector and
the gnomonic projection of the refracted sky (corresponding to
reverse transforms of D,A,C
in the RSCS
 ICS mapping of Chapter 2).
We assume independfent polynomial fits in
ICS mapping of Chapter 2).
We assume independfent polynomial fits in  and
and 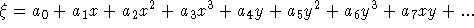 :
:
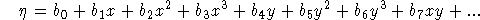

- Absolute Astrometry:
- Celestial coordinates tied to a fundamental
system, and the procedures for determining such coordinates.
Flux Calibration:
[To be written]
Defringing:
[To be written]
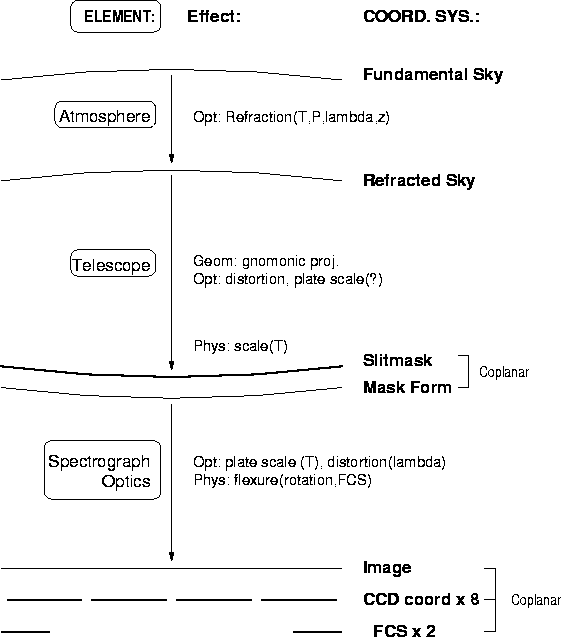
Astrometry: There are three levels of astrometry, all
using astrometric mapping (CCDCSi  ICS
ICS  FKCS)
that will be available from the database. The first level uses telescope
telescope pointing information from the image header -- expected relative
accuracy should be good to [
FKCS)
that will be available from the database. The first level uses telescope
telescope pointing information from the image header -- expected relative
accuracy should be good to [ 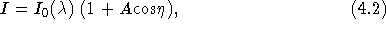 1 arcsec] ignoring differential
refraction and aberration; absolute accuracy is poor [
1 arcsec] ignoring differential
refraction and aberration; absolute accuracy is poor [ 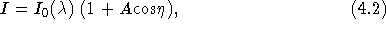 10 arcsec].
The second level adds the measurement of one star (or more) of known
coordinates -- this improves the absolute accuracy to the level of
relative accuracy [
10 arcsec].
The second level adds the measurement of one star (or more) of known
coordinates -- this improves the absolute accuracy to the level of
relative accuracy [ 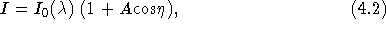 1 arcsec]. The third level requires three or more
astrometric reference stars in the image, and provides a correction to
the database astrometric mapping. The precision of this level is
the minimum required for slitmask design. It is expected that three
reference stars will be adequate to obtain
1 arcsec]. The third level requires three or more
astrometric reference stars in the image, and provides a correction to
the database astrometric mapping. The precision of this level is
the minimum required for slitmask design. It is expected that three
reference stars will be adequate to obtain 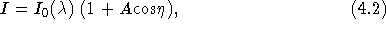 0.1 arcsec accuracy.
[Review all the accuracy estimates. The biggest unknown here is
the exact pixel scale, and whether it will vary with
0.1 arcsec accuracy.
[Review all the accuracy estimates. The biggest unknown here is
the exact pixel scale, and whether it will vary with  and/or focus.]
and/or focus.]
In the following, ``relevant'' refers to images and constants that are
associated with the filter used in the observation.
- Relative flux calibration (Flat-fielding): Retrieve the relevant
flat-field image from the database; divide.
- Defringing:
Retrieve relevant fringe frame from database; fit to sky fringes by scaling;
subtract.
- Absolute flux calibration: Retrieve the relevant constants
(zeropoint and extinction coefficient) from the database;
calculate the constant of proportionality (
 );
place constant in the header for use by analysis applications.
[What about gain - should this be included??
);
place constant in the header for use by analysis applications.
[What about gain - should this be included??
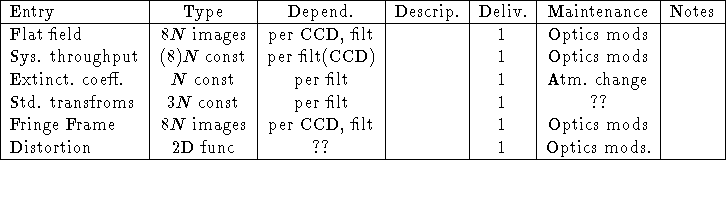
A library of standard flat-field frames through each filter will be
maintained for each CCD. [In practice, this may be a product of
pixel-to-pixel flats and large-scale flats.]
Nominal system throughputs for each filter will be maintained in the database.
Standard extinction values for Mauna Kea will be maintained in database.
Transforms from instrumental to standard photometric systems will be maintained
in database.
If useful/stable, a library of fringe frames for the night sky will be
maintained for each filter.
Distortion mappings will be maintained in the database.

NOTES -- Delivery: 0=Commissioning, 1=Pipeline.
Required Hardware:
- grid-of-holes (GOH) mask for differential distortion map.
For each filter:
- 1.
- Take 3 or more twilight flat frames with adequate exposure.
The telescope should be tracking during this sequence, but offset between
exposures.
- 2.
- Reduce each through bias-level correction.
- 3.
- Combine by taking the median level at each pixel (or use some
other robust level determinator that rejects cosmic rays). The individual
flats should be scaled by their mean/median levels in a cosmetically clean
region before combining, to remove differences in sky intensity.
- 4.
- Normalize to unity at the normalization point.
Advantages: Straight-forward; illumination by sky; better
``color balance.''
Disadvantages: Difficult to obtain images with proper exposures
(a model of sky counts per filter per sun altitude would help!); narrow
time window; stars in field often leave residual features.
In the above, adequate exposure depends on the accuracy desired. Usually
;SPMlt;1% accuracy is the goal, which means 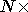 electrons level in each
image is adequate.
electrons level in each
image is adequate.
For each filter:
- 1.
- Take N dome flat frames with adequate exposure.
- 2.
- Reduce each through bias-level correction.
- 3.
- Combine by taking the median level at each pixel (or use some
other robust level determinator that rejects cosmic rays). The individual
flats should be scaled by their mean/median levels in a cosmetically clean
region before combining, to remove fluctuations in lamp intensity.
- 4.
- Remove large-scale variations by dividing the combined image by
a heavily smoothed version of itself -- this leaves a normalized image of
pixel-to-pixel variations (``pixel-to-pixel flat'').
- 5.
- Obtain one (or more) twilight flat(s). (Combine multiple images
by first scaling to same level, then taking median value at each pixel.)
Smooth and/or spatially-median filter
or fit by a surface to retain only large-scale variations
(``large scale flat'').
- 6.
- Multiply the large scale flat by the pixel-to-pixel flat.
- 7.
- Normalize to unity at the normalization point.
Advantages: Dome flats easy to acquire; pixel-to-pixel variations
can be monitored and combined with large scale flats to update the database
more often.
Disadvantages: Color balance not as good as with sky.
As above,
a goal of ;SPMlt;1% accuracy requires 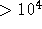 (electron level)
(electron level) 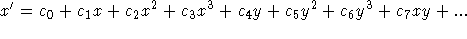 .
.
For each filter:
- 1.
- Take 3 or more deep frames in darktime with significant sky counts.
The telescope should be tracking during this sequence, but offset between
exposures. The field should contain as few stars as possible.
- 2.
- Reduce each through relative flux calibration.
- 3.
- Combine by taking the median level at each pixel (or use some
other robust level determinator that rejects stars and cosmic rays).
The individual
frames should be scaled (or offset?) by their mean/median sky levels.
- 4.
- Smooth on scales of a quarter the fringe wavelength.
- 5.
- Normalize to unity.
For each filter:
- 1.
- Take exposures of N photometric standard stars of varying
spectral type; process through relative flux calibration.
- 2.
- Determine the count rate for each standard star. Adjust for expected
atmospheric extinction. (Adjust for gain.)
- 3.
- [?? The method of defining the instrumental system has
not been investigated yet.]
- 1.
- Take one or more images of an astrometric field; process through
relative flux calibration.
- 1a.
- Take one or more images of the grid-of-holes mask before/after
to allow for future differential updates (dome or twilight sky illumination).
- 2.
- Measure the pixel positions of stars with known celestial
coordinates.
- 3.
- Fit the pixel coordinates to the gnomonic projections of
refracted sky coordinates; fit the same sky coordinates to the pixel
coordinates. [Functional form not yet known, but probably low-order
polynomial will be fine.]
- 1.
- Take one or more images of the grid-of-holes mask (dome
or twilight sky illumination).
- 2.
- Measure the pixel positions of holes in mask; compare with
previous grid-of-holes measurements.
- 3.
- Fit the differences in pixel location; this becomes the differential
update to be used in conjuction with the distortion map.
Instrument-control scripts and instructions to create the database products
listed above will be required.
What are the standard DEIMOS filters? Do instrumental-standard conversions
exist for filters of these specific design? Should the zeropoints follow
Johnson, AB, or some other magnitude system?
What are the extinction values for MK? (See Keck Web pages)
Do we want a more elaborate scheme for characterizing the color dependence of
pixel-to-pixel variations? This could be done spectroscopically.
There is no discussion of fringing here. This awaits analysis of fringing data.
Is distortion mapping the same for all filters, modulo scale change? This
can be checked with grid-of-holes comparisons in different filters.
[The role of gain is not fully developed in absolute flux cal
discussions.]
We need to discuss the effect of spatial distortion (different pixel scales
throughout the image) on flux calibration. If the distortion is
mapable (it should be!), there is no problem correcting the data for this.
How wide is the time window for twilight flats? How many filters can
we expect to do in each window?





Next: 8 Spectroscopy - Procedures
Up: Part III: DEIMOS Calibration:
Previous: 6 CCDs - Procedures
DEIMOS Software Team <deimos@ucolick.org>
1997-06-13T00:18:19
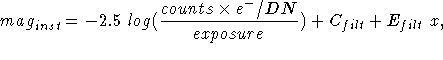 ).
The defining relation is:
).
The defining relation is:
![]()
![]() , sometimes refered to as total throughput
, sometimes refered to as total throughput![]() ,
contains all the information about system efficiency or
throughput for the normalization point of the flat-field image.
,
contains all the information about system efficiency or
throughput for the normalization point of the flat-field image.
![]()
![]() ,
, ![]() and
and ![]() can be deduced from observations of
standard stars, or ``synthesized'' using measured transmission curves
and published spectral energy distributions for a wide range of spectral
types.
can be deduced from observations of
standard stars, or ``synthesized'' using measured transmission curves
and published spectral energy distributions for a wide range of spectral
types.
 ICS mapping of Chapter 2).
We assume independfent polynomial fits in
ICS mapping of Chapter 2).
We assume independfent polynomial fits in ![]()
![]()
 );
place constant in the header for use by analysis applications.
[What about gain - should this be included??
);
place constant in the header for use by analysis applications.
[What about gain - should this be included??