To discuss calibrations, we first need to define several coordinate
systems, enumerate potential variables and dependencies for each one,
and describe how we will map from one to the next (see Figure 2.1).
A mapping from one (two-dimensional) coordinate system to another consists of
the following elements![]() :
:
Figure 2.1: Coordinate Systems - Overview
This section briefly sketches how each of these elements will be determined, with more details to follow in Section 2.2 and Chapters 5, 7 and 8.
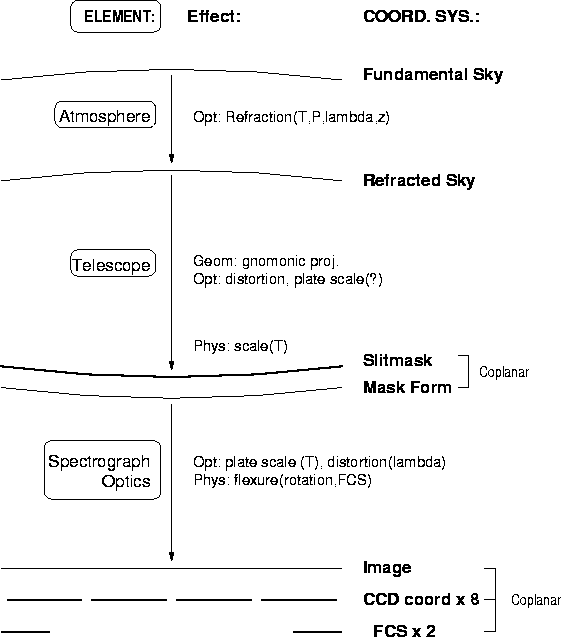 RSCS
depends on atmospheric pressure and temperature, observed wavelength,
and zenith distance (neglected dependencies include humidity)
and will be provided by standard models of refraction.
RSCS
depends on atmospheric pressure and temperature, observed wavelength,
and zenith distance (neglected dependencies include humidity)
and will be provided by standard models of refraction.
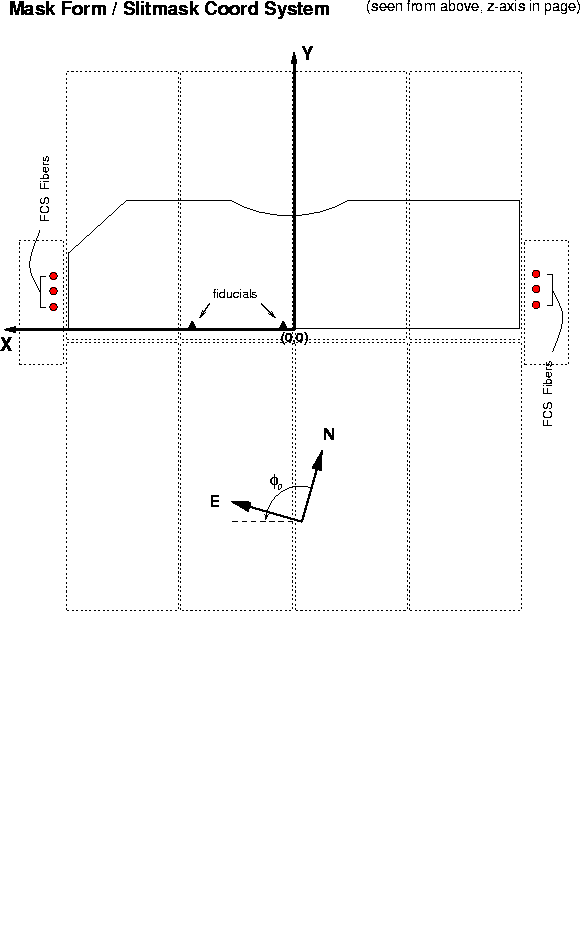 m). For most purposes,
these two systems can be considered identical and will
be referred to as MF/SMCS (Figure 2.2).
The SMCS is a rectilinear x,y system defined on the flat slitmask stock.
Its fiducials
are the edges of the mask that rest against mounting stops on the mill
and on the slitmask form. There is a dependency on slitmask temperature,
so the SMCS is defined for the nominal operating temperature.
The mapping RSCS
m). For most purposes,
these two systems can be considered identical and will
be referred to as MF/SMCS (Figure 2.2).
The SMCS is a rectilinear x,y system defined on the flat slitmask stock.
Its fiducials
are the edges of the mask that rest against mounting stops on the mill
and on the slitmask form. There is a dependency on slitmask temperature,
so the SMCS is defined for the nominal operating temperature.
The mapping RSCS  MF/SMCS is determined to first order
by the known mapping of the refracted sky onto the telescope Nasmyth focal plane,
and thence by projection of the focal plane onto the tilted cylindrical
slitmask. This first-order mapping is tuned by observations of
astrometric standard star fields through astrometric masks.
MF/SMCS is determined to first order
by the known mapping of the refracted sky onto the telescope Nasmyth focal plane,
and thence by projection of the focal plane onto the tilted cylindrical
slitmask. This first-order mapping is tuned by observations of
astrometric standard star fields through astrometric masks.
Figure 2.2: Mask Form / Slitmask Coordinate System, (MF/SMCS)
 ICS is determined
by measuring the individual mappings MF/SMCS
ICS is determined
by measuring the individual mappings MF/SMCS  CCDi
(see below), corrected back to the ICS using the mappings
CCDi
CCDi
(see below), corrected back to the ICS using the mappings
CCDi  ICS (see below).
ICS (see below).  ICS mappings,
one for direct imaging and one for spectroscopy.
Each filter and (grating+tilt) has its own mapping.
The direct imaging mappings consist of scale and distortion terms only
(since the orientation and zeropoint of the ICS were defined above). These
are determined by direct images of a special slitmask
with a finely and accurately milled grid of small holes
(grid-of-holes mask, GOH). The direct imaging mappings
involve only CCDs 1-4. The spectroscopy mappings involve a
wavelength function that maps pixel coordinates onto
ICS mappings,
one for direct imaging and one for spectroscopy.
Each filter and (grating+tilt) has its own mapping.
The direct imaging mappings consist of scale and distortion terms only
(since the orientation and zeropoint of the ICS were defined above). These
are determined by direct images of a special slitmask
with a finely and accurately milled grid of small holes
(grid-of-holes mask, GOH). The direct imaging mappings
involve only CCDs 1-4. The spectroscopy mappings involve a
wavelength function that maps pixel coordinates onto
Figure 2.3: Image Coordinate System, (ICS)
 CCDCSi consist of the rotation
and displacement
of each CCD from the idealized focal plane coordinate system, ICS. These
quantities are determined for CCDs 1-4 from direct images of the
above-mentioned grid-of-holes mask.
To extend this information to CCDs 5-8, an arc spectrum is taken through
the line of holes (LOH) mask. The known rotations and displacements
of CCDs 1-4 from part A are corrected to create the lower half of the
idealized, seamless ICS focal plane. The spectral traces (x-heights)
and
CCDCSi consist of the rotation
and displacement
of each CCD from the idealized focal plane coordinate system, ICS. These
quantities are determined for CCDs 1-4 from direct images of the
above-mentioned grid-of-holes mask.
To extend this information to CCDs 5-8, an arc spectrum is taken through
the line of holes (LOH) mask. The known rotations and displacements
of CCDs 1-4 from part A are corrected to create the lower half of the
idealized, seamless ICS focal plane. The spectral traces (x-heights)
and

 MF/SMCS and TVCS
MF/SMCS and TVCS  RSCS, but, since
RSCS
RSCS, but, since
RSCS  MF/SMCS is already known, the single mapping MF/SMCS
MF/SMCS is already known, the single mapping MF/SMCS  TVCS
suffices. The zeropoint and orientation of this mapping are provided by the
visible pair of fiducials, whose measured pixel locations,
continuously updated, allow constant correction for TV flexure.
Guiding thus maintains constant guidestar position
relative to DEIMOS' focal plane rather than relative to the TV pixels.
Scale and higher-order distortion terms in MF/SMCS
TVCS
suffices. The zeropoint and orientation of this mapping are provided by the
visible pair of fiducials, whose measured pixel locations,
continuously updated, allow constant correction for TV flexure.
Guiding thus maintains constant guidestar position
relative to DEIMOS' focal plane rather than relative to the TV pixels.
Scale and higher-order distortion terms in MF/SMCS  TVCS
are provided by calibration images of astrometric standard star fields.
[...if needed.]
Separate mappings MF/SMCS
TVCS
are provided by calibration images of astrometric standard star fields.
[...if needed.]
Separate mappings MF/SMCS  TVCS
are needed for each TV filter. They may also depend on temperature.
TVCS
are needed for each TV filter. They may also depend on temperature.
[a lot changed above - must be reviewed for consistency later on. Also, TV, FCS figures must be created. And two more figures below.]
For most of these coordinate systems,
the definition of the cardinal axes corresponds to the global coordinate
axes of the DEIMOS design (see Figures ?? and ?? for the global and individual
DEIMOS' coordinate systems).
All x-axes point in a set direction (``up'' in Figure ??), normal to
the light path, the local z-axis is always in the direction of photon travel, and the
y-axes generally point ``outboard''. However, this last
convention is inverted for the ICS and CCDCSi coordinate
systems, whose y-axes point inboard (see Figure 2.3).
The ICS is the
coordinate system that the observer sees on the quick-look
display, where it has (0,0) in the lower left corner with x increasing
to the right and y upwards. It is also defined so
that positive y points towards increasing ![]() along the
spectrum and the display shows a direct view of
the sky for direct imaging (see Figure 2.3). These constraints
require that the y-axis reverse direction in the ICS and
CCDCSi coordinate systems.
along the
spectrum and the display shows a direct view of
the sky for direct imaging (see Figure 2.3). These constraints
require that the y-axis reverse direction in the ICS and
CCDCSi coordinate systems.
The fundamental sky coordinates can be described in any equinox and epoch.
To update and refract to observed coordinates on the sky,
four transforms are needed, to account for
(1) proper motion;
(2) precession;
(3) aberration of starlight![]() ; and
(4) atmospheric refraction:
; and
(4) atmospheric refraction:
![]()
![]()
![]()
![]()
where ![]() are the updated, refracted
coordinates of the fundamental sky
are the updated, refracted
coordinates of the fundamental sky ![]() at the zenith distance z, wavelength
at the zenith distance z, wavelength ![]() ,
and atmospheric temperature and pressure,
,
and atmospheric temperature and pressure, ![]() .
.
These are all standard transformations, and will be taken from the Starlink SLAlibhttp://star-www.rl.ac.uk/ library.
This mapping is performed in three stages: first, a gnomonic projection
is made of the [refracted] sky; second, an adjustment is made in the
radial direction for distortion; and lastly a projection onto
the tilted, curved surface of the mask![]() .
Due to the format of the distortion mapping from ray-tracing programs, these
take the form:
.
Due to the format of the distortion mapping from ray-tracing programs, these
take the form:
![]()
![]()
![]()
where ![]() are the physical coords projected onto the
tilted, cylindrical surface of the mask (described by a tilt,
are the physical coords projected onto the
tilted, cylindrical surface of the mask (described by a tilt, ![]() , and a
radius of curvature,
, and a
radius of curvature, ![]() );
); ![]() are the standard
coordinates produced by a gnomonic projection of
are the standard
coordinates produced by a gnomonic projection of ![]() at
position angle
at
position angle 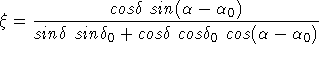 , converted to off-axis angles on the sky.
The position angle of the mask,
, converted to off-axis angles on the sky.
The position angle of the mask, 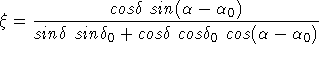 , is defined as the position angle of
the x-axis on the sky.
, is defined as the position angle of
the x-axis on the sky.
The gnomonic projection is:
![]()
![]()
These are tangents; rotation so that ![]() is parallel to the
y-axis and converting to angles:
is parallel to the
y-axis and converting to angles:
![]()
![]()
where 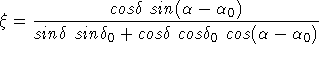 is the position angle of the x-axis on the sky.
is the position angle of the x-axis on the sky.
The mapping from the off-axis angles to the projected physical coordinates,
![]() ,
is determined via ray-tracing
,
is determined via ray-tracing![]() .
It is best determined using image centroids rather than principle rays.
.
It is best determined using image centroids rather than principle rays.
The mapping from the projected physical coordinates to the tilted, cylindrical surface is:
![]()
![]()
![]()
The value 135mm above is a zeropoint offset, that is, the value of ![]() where
where ![]() and
and ![]() .
.
In addition, the tilted and curved surface produces a modification
to position angle ![]() with respect to the x-axis
(
with respect to the x-axis
( 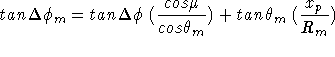 ), given by
), given by
![]()
This mapping is performed in three stages: first, a projection from the tilted, curved slitmask to a plane; secondly, conversion into input angles at the grating/mirror; then mapping with the camera distortions to the camera focus.
![]()

![]()
where ![]() and
and 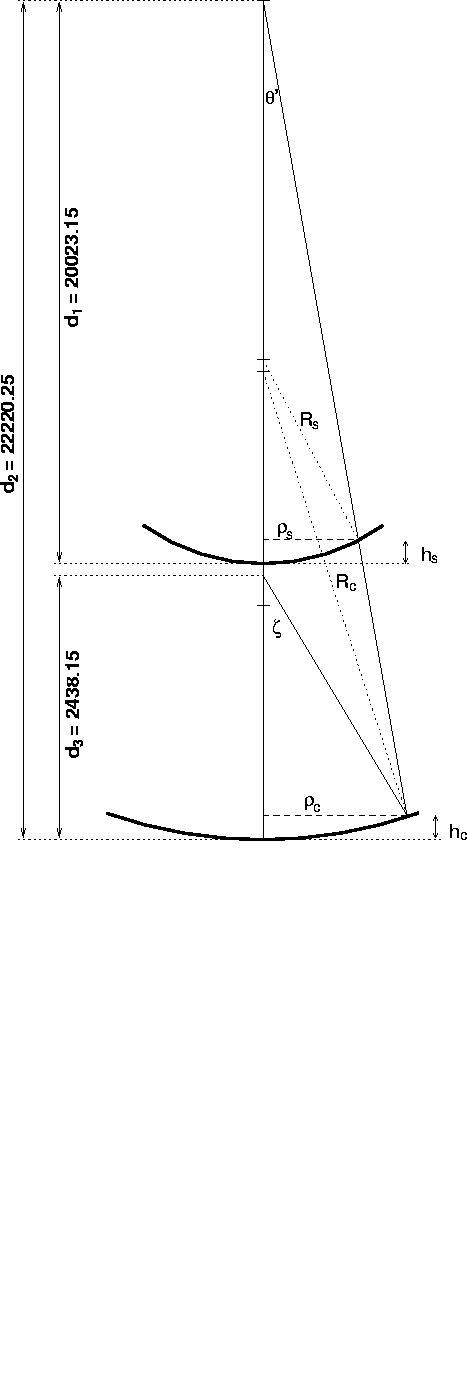 are various fixed pupil distances and
radii (see Figure 2.4).
are various fixed pupil distances and
radii (see Figure 2.4).
Figure 2.4: Schematic of rays, telescope through collimator
The first mapping is a reverse of the earlier projection:
![]()
![]()
![]()
The second mapping to input angles depends on the axial radii and heights, both at the image surface (slitmask) and the collimator.
![]()
![]()
![]()
where ![]() and
and 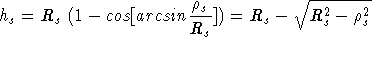 are the heights of the image and collimator
surfaces:
are the heights of the image and collimator
surfaces:
![]()
![]()
For rough estimates, ![]() and
and 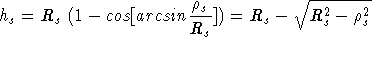 can be ignored. In practice,
the approximation for
can be ignored. In practice,
the approximation for  is probably sufficiently adequate,
although for highest precision and computational speed,
it is probably best to provide a table
of precise
is probably sufficiently adequate,
although for highest precision and computational speed,
it is probably best to provide a table
of precise ![]() values and interpolate for specific
values and interpolate for specific ![]() .
.
The axial angles ![]() are converted into incident angles at the
grating by
are converted into incident angles at the
grating by
![]()
![]()
where ![]() is the tent mirror angle and
is the tent mirror angle and 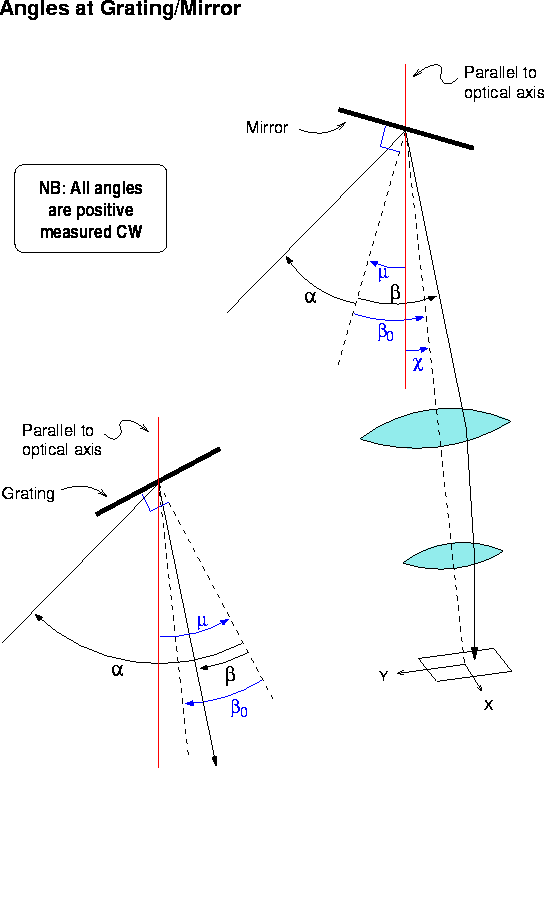 the angle of the grating normal, both with respect to the optical axis.
the angle of the grating normal, both with respect to the optical axis.
The third mapping is straightforward, although it includes factors for camera distortion which are available from ray-tracing (but may need to be determined empirically?). In the following, the angles and their sense are given in Figure 2.5.
Figure 2.5: Schematic of rays, grating to detector
![]()
![]()
![]()
where ![]() is the camera angle with respect to the collimator optical
axis. Note that
is the camera angle with respect to the collimator optical
axis. Note that ![]() are measured with respect to the optical axis
of the camera.
are measured with respect to the optical axis
of the camera.
With the mirror in place, incident and reflected angles are equal in magnitude but opposite in sense:
![]()
With a grating in place:
![]()
where m is the order, usually first, n is the index of refraction
of air, and ![]() is the spacing of rulings on the grating.
is the spacing of rulings on the grating.
Note that the third mapping is usually needed in reverse, in order to
estimate a ![]() for a given pixel location:
for a given pixel location:
![]()
![]()
This mapping involves rotation and translation constants for each of the eight CCDs in the mosaic. CCDCSi will generally be expressed in pixels.
![]()
![]()
where ![]() is the rotation and
is the rotation and 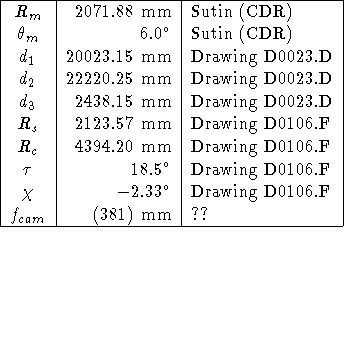 are the
translations for each CCD with respect to the ICS.
Note that even the fiducial CCD can have a rotation and offset with respect
to the ICS, which by definition has axes parallel to those of the MFCS.
are the
translations for each CCD with respect to the ICS.
Note that even the fiducial CCD can have a rotation and offset with respect
to the ICS, which by definition has axes parallel to those of the MFCS.
[Not yet described.]
Engineering drawings currently give the following values:
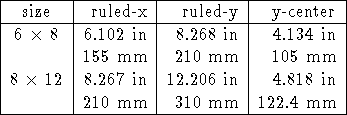
The following grating parameters will also be of interest when discussing vignetting:
![]()
[We need to make some direct mappings between non-adjacent coordinate systems, as in astrometry off direct images, and the definitions from the theoretical mappings above do not describe these well. Furthermore, these mappings must be made empirically, although the analytic mappings may be used in many cases to provide estimates of their form and scales. These are the mappings that will be discussed:
 CCDCDi. Although discussed above, we must
measure the actual
CCDCDi. Although discussed above, we must
measure the actual